 Home
Home
 Back
Back
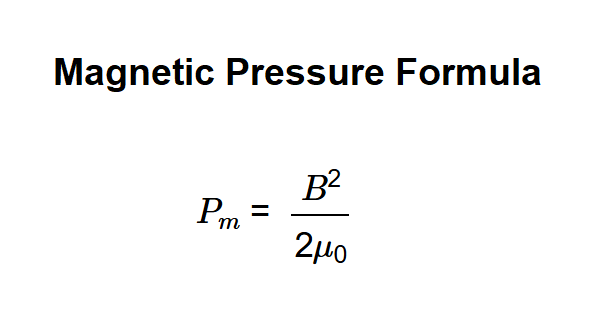
Definition: This calculator computes the magnetic pressure (\( P_m \)) in a magnetic field based on the formula \( P_m = \frac{B^2}{2 \mu_0} \), where \( B \) is the magnetic field strength and \( \mu_0 \) is the magnetic permeability of free space (\( 4\pi \times 10^{-7} \) H/m).
Purpose: It helps physicists, engineers, and scientists analyze magnetic forces in applications like plasma physics, magnetic confinement fusion, and electromagnetism, particularly for understanding pressure exerted by magnetic fields.
Calculations are based on the magnetic pressure formula:
Unit Conversions:
| Category | Unit | Conversion to SI Unit |
|---|---|---|
| Magnetic Pressure | Pa (Pascals) | 1 Pa |
| bar | 1 bar = 100,000 Pa | |
| psi (Pounds per square inch) | 1 psi = 6894.76 Pa | |
| at (Technical atmospheres) | 1 at = 98,066.5 Pa | |
| atm (Standard atmospheres) | 1 atm = 101,325 Pa | |
| Torr | 1 Torr = 133.322 Pa | |
| hPa (Hectopascals) | 1 hPa = 100 Pa | |
| kPa (Kilopascals) | 1 kPa = 1000 Pa | |
| MPa (Megapascals) | 1 MPa = 1,000,000 Pa | |
| inHg (Inches of mercury) | 1 inHg = 3386.39 Pa | |
| Magnetic Field (B) | uT (Microteslas) | 1 uT = 10⁻⁶ T |
| mT (Milliteslas) | 1 mT = 10⁻³ T | |
| T (Teslas) | 1 T | |
| GT (Gigateslas) | 1 GT = 10⁹ T | |
| G (Gauss) | 1 G = 0.0001 T |
Details: Accurate magnetic pressure calculations are crucial for understanding the forces exerted by magnetic fields in plasma physics, fusion reactors, and electromagnetic devices, ensuring proper design and operation in scientific and engineering applications.
Tips: Enter Magnetic Field (uT, mT, T, GT, G). Results include magnetic pressure in multiple units (Pa, bar, psi, at, atm, Torr, hPa, kPa, MPa, inHg).
Notes: Magnetic pressure is the pressure exerted by a magnetic field on a medium, particularly in plasmas or ferromagnetic materials. The magnetic permeability of free space (\( \mu_0 \)) is fixed at \( 4\pi \times 10^{-7} \) H/m, and the magnetic field strength must be positive.